Scalar product of vectors online calculator
Scalar product of the vectors is the product of their magnitudes (lengths) and cosine of angle between them:
The above formula reads as follows: the scalar product of the vectors is scalar (number). In addition, scalar product holds the following features:
Commutativity:
Associativity, relative to scalar multiplier ():
Distributivity:
Two non-zero vectors are perpendicular if and only if their scalar product equals to zero:
In the coordinate form, scalar product of two vectors is expressed by the formula:
, where and .
Our online calculator is able to find scalar product of two vectors with step by step solution.
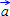 by:
by: 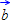 by:
by: 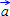 = { }
= { }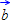 = { }
= { }See also:
Solve equations online calculatorSeries convergence solver
Scalar triple product of vectors online
Volume of solid of revolution online