Проверить образуют ли вектора базис онлайн калькулятор
Базисом в -мерном пространстве называется упорядоченная система из линейно-независимых векторов.
Введём также некоторые дополнительные понятия, необходимые для дальнейшего изложения.
Выражение вида:
, где − некоторые числа и называется линейной комбинацией векторов .
Если существуют такие числа из которых хотя бы одно не равно нулю (например ) и при этом выполняется равенство:
, то система векторов − является линейно-зависимой.
Если же указанное равенство выполняется лишь при условии, что все числа , тогда система векторов − является линейно-независимой.
Базис может образовывать только линейно-независимая система векторов. Понятие линейной зависимости/независимости системы векторов, тесно связано с понятием ранга матрицы.
Наш онлайн калькулятор позволяет проверить образует ли система векторов базис. При этом калькулятор выдаёт подробное решение на русском языке.
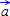 1 по:
1 по: 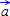 2 по:
2 по: 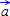 3 по:
3 по: 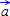 4 по:
4 по: 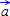 5 по:
5 по: 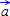 6 по:
6 по: 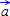 7 по:
7 по: 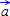 8 по:
8 по: 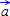 9 по:
9 по: 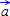 1 = { }
1 = { }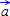 2 = { }
2 = { }Другие полезные разделы:
Объём параллелепипеда, построенного на векторахОбъём тетраэдра, построенного на векторах